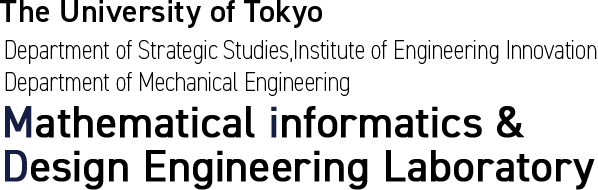Research

HOME > Research

Research Introduction Video

Going beyond the framework of topology optimization to the generation of mechanical systems

Structural optimization is a structural design method based on mathematics and mechanics. The structural optimization methods are classified as sizing, shape and topology optimization as shown in figure 1. Especially, topology optimization has the highest design freedom among these methods. We have presented a novel topology optimization method based on the level set method to overcome several issues in traditional approaches.

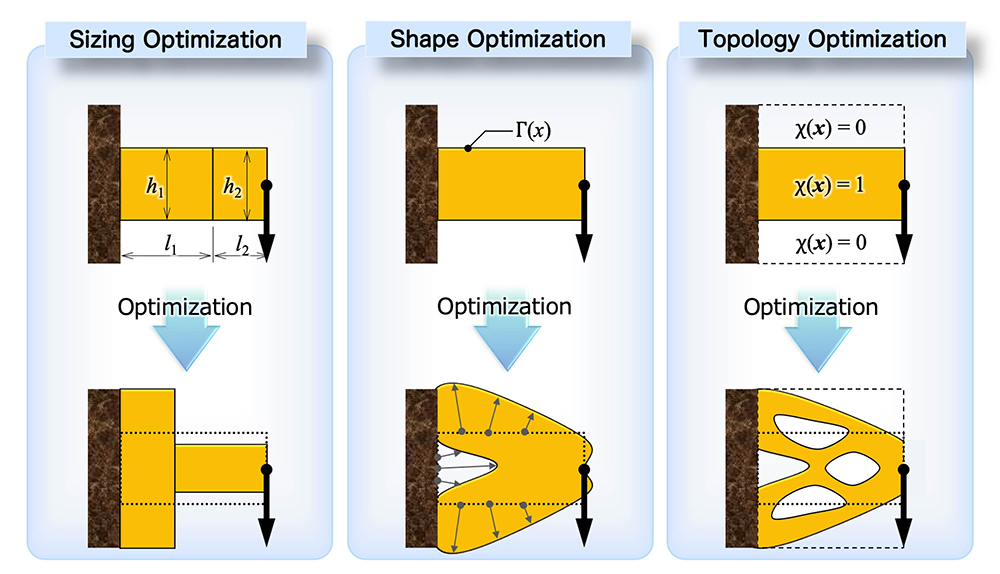
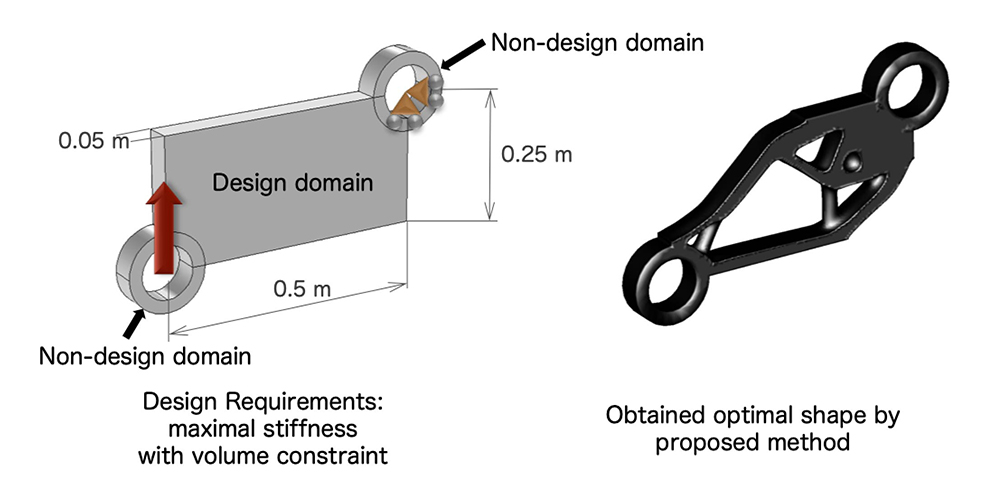
Figure1 Schematic diagram of the case where each structural optimization method is applied to a cantilevered beam with the left end fixed and the right end-loaded downward to the center.
Figure2 Topology optimization based on the level set method applied to the design problem of mechanical structural components

Additionally, based on our method, we have presented several optimum design methods, such as actuators design, wing design of an airplane, maximizing eigenfrequency problem, material design with negative Poisson’s ratio, cloaking device design, and heat device design.
However, all of them have been limited to the downstream design phase of the design, such as the design of a single device or material structure, and have not resulted in a design that considers the entire mechanical system. In the future, we are working on the construction of a design theory that can generate the entire mechanical system, including a multi-phase design theory that takes each design phase into account.

Related Papers

  • ● Level set-based topology optimization
    Comput. Meth. Appl. Mech. Eng., (2010) 199(45-48), pp. 2876-2891. DOI. Preprint.

An integrated theory of mechanics, design, and manufacturing

Although topology optimization can generate design solutions based on physics and mathematics, it often results in design solutions with geometrical complex substructures. Therefore, when manufacturing and assembly processes are taken into account, the design solution obtained by topology optimization is not an engineering-appropriate design solution and is not an optimal design solution from an engineering perspective. In this laboratory, we are conducting "Construction of geometric mathematical models for design and production and optimization of design and production systems" and "Development of mathematical models for various design phases and production requirements" in order to construct methodologies to create optimal design solutions from an engineering perspective.

Topology optimization based on the premise of molding with molds

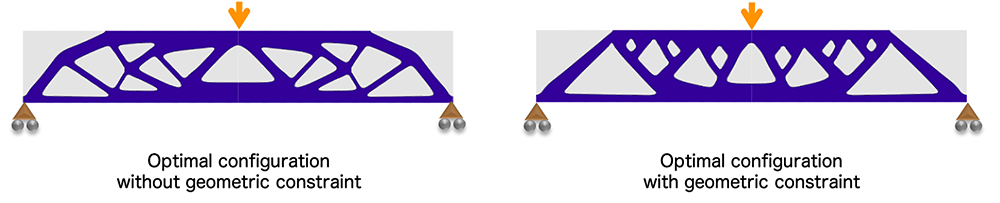
Topology optimization based on maximum tilt angle for metal additive manufacturing

Related Paper

  • ● A fictious physical model to evaluate manufacturability
    Int. J. Adv. Manufact. Tech., (2017) 92(1-4), pp. 1391-1409. DOI. Preprint.
  • ● mathematical model for geometric features
    J. Comput. Design & Eng., (2019) 6(4), pp.647-656. DOI.

Discover extraordinary devices and materials

In recent years, man-made materials, called metamaterials, have attracted much attention for their unique properties that homogeneous materials in nature do not exhibit.

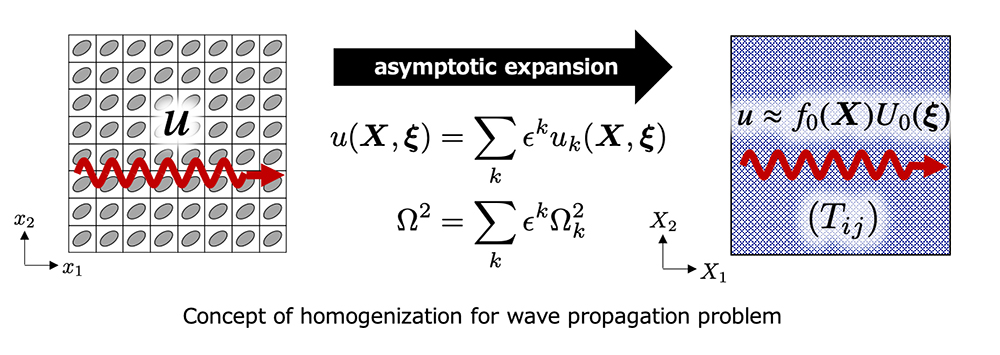
We have been developing metamaterials with novel functions and mechanisms for a wide range of physical phenomena such as wave propagation problems, heat propagation problems, and fluid problems. For this purpose, we introduce multiscale analysis methods, mainly homogenization methods, which can efficiently evaluate the performance of metamaterials, and topology optimization.

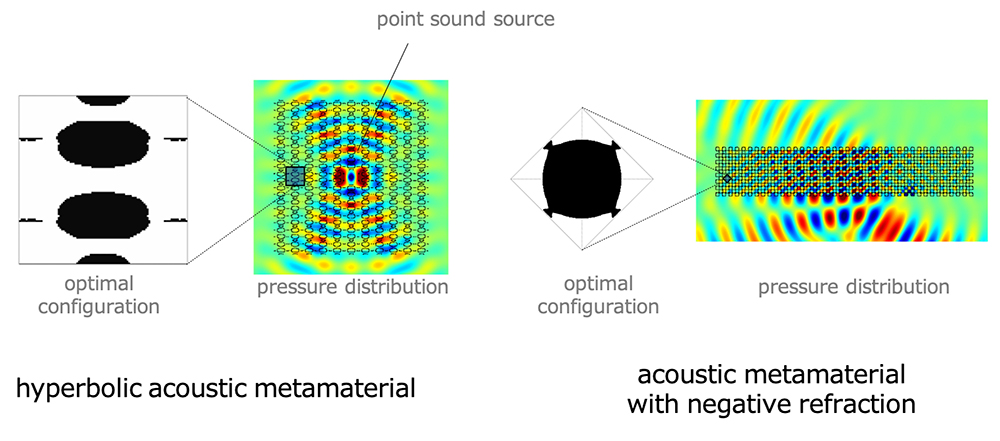
Optimum design of metamaterials based on the homogenization method

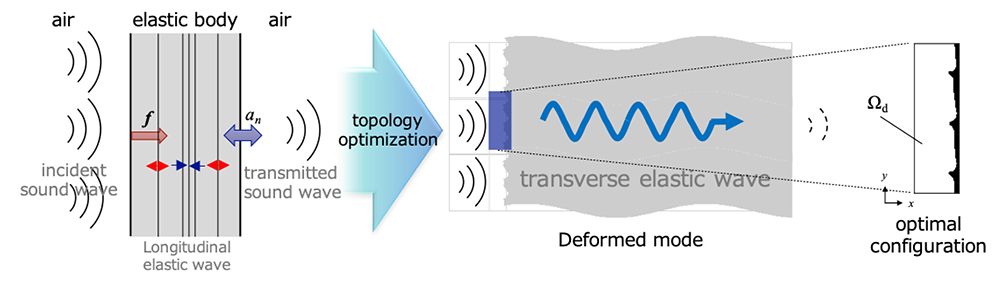
Metamaterials with complex geometries can be efficiently characterized by replacing them with homogeneous materials with effective material constants Tij.

Wave motion converting metasurface：

A soundproofing effect can be expected by converting longitudinal sound waves into transverse elastic waves.

Related　papers

  • ● Wave motion converting metasurface
    Appl. Phys. Lett., (2015) 107(22), p. 221909. DOI. Preprint.
  • ● Hyperbolic acoustic metamaterial
    Comput. Meth. Appl. Mech. Eng., (2018) 335, pp. 419-471. DOI. Preprint.
  • ● Heat-driven pump with molecular gas effect
    J. of Comput. Phys., (2019) 395(15), pp. 60-84. DOI. Preprint.
  • ● Cloaking for optics
    Appl. Phys. Lett., (2013) 102(25), p. 251106. DOI. Preprint.